【機械学習基礎固め】線形回帰(Linear Regression)の初歩的ポイントを再確認して書いておく
昨年の今頃、CourseraのMachine Learningの講座を受講しましたが、 急いで詰め込んだ情報ってのは、やっぱり消えていくのも早いようです。

当時、仕事で炎上案件の火消し作業に関わっておりまして、 深夜に帰宅し、晩御飯をいただきながらネットで受講。 字幕付きの英語のビデオを視聴して、週一で課題提出というサイクル。 特に後半は睡眠時間の確保が難しくなり気持ち的にも駆け足で、次第に「講座を終わらせること」が目的になっていました。
どうにか8月末に修了したけど、達成感とか感じる前に「炎上案件なんだかなあ?」な状況で、学習内容はすぐに蒸発。 理解が曖昧なところが起点になって、急速に知識の最小単位の輪郭がぼやけていくんですよ怖い怖い。
てなことで、一年経って新たな気持ちで講座のテキストや受講中に取ったノートをめくりながら復習中。 気長にじっくりポイント押さえて経年劣化の激しいニューラルネットワークにしっかり刻みつけていきたいなあと思っております。 ただし、ここに書いているのは私個人が理解したと思っているものに過ぎませんので気を付けてくださいね。
以下の記事では、実際に線形回帰をやってみています。結果はいまいち満足していないですが、ご参考に。
ちなみに、数式はMathJax使って書いています。LaTeXの書式で数式を書けば、きれいに整形してくれるスクリプト。まともに使ったことがなかったのですが、なかなか便利。ブログはMarkdownで書いているので _や^を\でエスケープしないといけないようで少々わずらわしいのですが、理屈が分かればなんとかなります。
やはり、いくつになってもお勉強です。
- Courseraの権利を侵害するのはまずいので、本記事の内容は箇条書きに毛が生えた程度のものです。またテキストの内容をそのまま書いたりもしませんよ。
- 詳しい内容を知りたい方は、ぜひとも同講座を受講してみてくださいね。非常に興味深い内容です。
- 受講のためには、少なくとも、行列演算の基礎を理解している必要があると思います。それと課題や試験の文章が英語なので、辞書片手にでもよいので英文の読解力がある程度必要です。講義の動画では日本語の字幕が付きますが、私が受講したときは、字幕が追い付いていない場面が何か所かありました。また、字幕を読んでいる時は、表示されてる式を見逃すということも。ヒヤリングができるに越したことはないですよ。
- まあしかし、無料なので気軽に受けてみるのもアリかもしれない。構えて撃ってから狙いましょう。
ところで、Octave for Windowsの不便な点
ハナから横道に逸れますゴメンナサイ。先日からWindows 10でMinGW/MSYSからOctaveを使っていますが、不便な点が以下3つ。
gccでビルドすれば解決できそうな気がするのですが、またそのうち。
線形回帰(Linear regression)とはなんであるか
線形回帰(分析)とは、線形モデルによる回帰分析ということらしい。データセット内のデータの相関をモデル化する方法・・・かな?
線形モデルは、以下のような式で定義されます(Wikipediaから引用)。
\[ Y=\beta_{0} + \beta_{1}X_{1} + \beta_{2}X_{2} + \dots + \beta_{p}X_{p} + \varepsilon \]
\[ \begin{eqnarray*} Y & : & 出力値\\ X_i & : & 入力値\\ \beta_i & : & 線形モデルのパラメータ \end{eqnarray*} \]
実は自分、\(\varepsilon\)が何物なのか理解できていません。切片は\(\beta_{0}\)だし・・・。 まあ、とにかく、与えられたデータセットに対して、このような線形モデルの仮説を立てて、そのパラメータである\(\beta_i\)を決定しましょうということですね。
例えば、日毎の最高気温と湿度、アイスキャンデーの売上額というデータセットがあって、 ある日の天気予報から売上予測を行う場合、 最高気温は\(X_1\)、湿度は最高気温は\(X_2\)、売上額は\(Y\)ですが、\(\beta\)の値がわからない。 データセットは観測(測定)データであり、計算して出したものではありませんから。
てことで、与えられた実際のデータセットを線形回帰分析して、\(\beta_{0 \dots 2}\)をちょうどよい値に調整するということですね。
参考サイト
仮説関数(hypothesis function)
仮説関数。これは、与えられた問題を解決するための関数であって、いわゆる上で書いている線形モデルそのものですね。 既知のデータから作成された入力と出力の相関を表すための式ですから、実データXを与えれば実データY(に近い値)を出力し、未知の入力に対しても仮説に基づいた値を出力する。つまり、これを使って予測ができるということになる。
線形回帰では仮説関数が線形モデルになっているということですね。
上のWikipediaからの引用では、モデルのパラメータを\(\beta\)としていましたが、Courseraの講座では一貫して\(\theta\)で統一されていました。 自分にとってはすでにこちらのほうがなじみがあるので、以降\(\theta\)で通します。
講座では、以下のような単純な仮説が立てられていました。(\(x\)が入力。\(y\)は仮説に基づいて出力される値)
\[ y=\theta_0 + \theta_1x_1 + \theta_2x_2 \]
この仮説関数は、\(x_0 = 1\)と置くと以下のように書けます。
\[ y=\theta_0x_0 + \theta_1x_1 + \theta_2x_2 \]
そしてこれは行列を使用して以下のように記述できます。日常的に行列を扱っていないので、上の式を見てすぐ行列演算に結び付けられないが、それも慣れなのだろう。
\[ h_\theta(x) = \theta^{T}x = \theta_0 + {\theta_1}x_1 + {\theta_2}x_2 \]
\(\theta^{T}\)のTは転置(Transpose)の意味です。以下参照。
\[ \theta^T = {\begin{bmatrix} \theta_0\\ \theta_1\\ \theta_2 \end{bmatrix}}^T = \begin{bmatrix} \theta_0 &\theta_1 &\theta_2 \end{bmatrix} \]
\(\theta_{0 \dots 2}\)が、線形モデルのパラメータ(初期値は1とか乱数とか)。後述の勾配降下法によって、コスト関数の出力が少なくなる(つまり誤差が少ない)値を決定するのです。これが線形回帰分析ですね。
※ \(x_1\)の添え字の1は、最初の入力値という意味であり、データセットのインデックスではありません。
コスト関数(Cost function)
コスト関数は、仮説関数がどれくらい的を得ているかを表します。 実データと理論値の差分の絶対値に関する値で。 線形回帰では、たいてい以下の式で定義されるらしく、全サンプルの二乗平均誤差に比例する値です。
\[ J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} ({{h_\theta}{(x^{(i)})-y^{(i)}})^{2}} \]
下図は、Courseraの講座で描いたコスト関数の三次元グラフです。縦方向がコストです。

勾配降下法(Gradient Descent)
売り上げランキング: 34,160
線形回帰の目的は、コスト関数の結果を最小化する\(\theta\)を見つけること。 そのために、勾配降下法を使用して、線形回帰のパラメータである\(\theta\)を、データセットにフィットさせます。 勾配降下法にも種類があるようですが、最初はバッチ勾配降下法(Batch Gradient Descent)が取り上げられていました。 これまた「それが何たるや?」は、よくわかっていないので、そのうち確認してみます。 とりあえず、コスト関数\(J(\theta)\)の出力を最小化する\(\theta\)を見つける方法の一つということで。
その名のとおり、坂を下りていくようなアルゴリズム。x軸を\(\theta_0\)、y軸を\(\theta_1\)、z軸をコスト関数の出力として、x-yをスイープして描いた三次元のグラフについて、特定のx-y位置からz成分が小さくなる方向へ徐々に移動(\(\theta_0\)と\(\theta_1\)を更新)していくものです。最終的に逆向きのピークに落ち着くというわけですね。
下図は、講座の中で、コスト関数の等高線を描いたものです。赤い×印が一番コストの低い場所です。
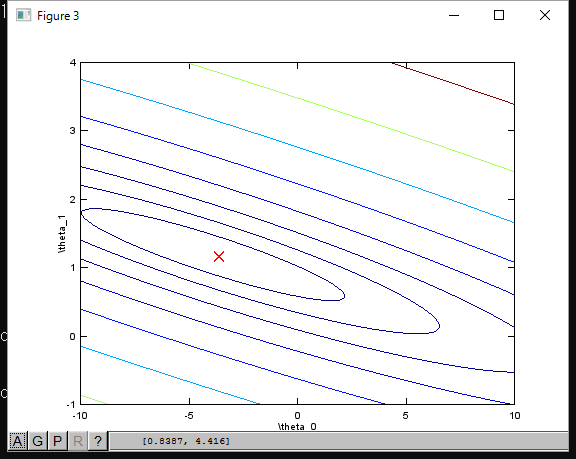
このように、データを可視化して、処理が正しく行われているかを確認する必要があります。 θの要素数が多い場合は全てを使ってグラフを描けませんが、特定の軸を抜き出して描けばよいです。勾配降下に関する考え方は同じです。 また、複雑な仮説関数では、くぼんでいるが、一番低いわけではない場所に落ち込んでしまう場合がありますが、そういった問題の回避方法や、速めに収束させるためのテクニックなどが講座で細かく紹介されていました。
線形回帰のパラメータθを繰り返し更新する
実際の演算ではθをスイープするのではなく(演算量が大きすぎるし意味がない)、ある出発地点を選んで、その場所のコスト/θの傾きに応じて、コストが低い場所へ移動することを繰り返します。
ある地点の傾きが関わってくるので、偏微分といった(自分的に)難しい内容も関連し、きちんと理解していませんが、とりあえず、個々の繰り返しでθを更新するのは、以下の式を使うらしい。
\[ \theta_j := \theta_j-\alpha \frac{1}{m} \sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_j \]
- \(i\)は、データセットのインデックス。
- \(j\)は、線形回帰パラメータの添え字。
- \(\alpha\)は学習率(learning rate)を表す値です。小さな値では\(\theta\)の収束が遅くなり、大きな値だと早く収束します。
ここで大切なのは、\(\theta\)の全要素を同時更新するということです。\(\theta\)の要素がひとつでも変化すると、仮説関数 \(h_\theta(x^{(i)})\) は別の式になり、その値は変化してしまいますが、全要素を更新するまで仮説関数は変化すべきではないということです。
繰り返しによって線形回帰のパラメータ\(\theta_j\)は、コスト関数\(J(\theta)\)を最小化する値に近づいていきます。
Octave/MATLABの使い方
CSVを読み込む
データセットがカンマ区切りのテキストデータとして用意されている場合、Octave/MATLABで以下のようにして行列に読み込みます。
data = load('data.csv'); % カンマ区切りのテキストデータを読み込む
例えばCSVにn列m行のデータがあるなら、dataの中身は以下のようになっています。
\[ data= \begin{bmatrix} d_11 &d_{21} &\dots &d_{(n-1)1} &d_{n1}\\ d_12 &d_{22} &\dots &d_{(n-1)2} &d_{nn2}\\ d_13 &d_{23} &\dots &d_{(n-1)3} &d_{n3}\\ \vdots &\vdots &\vdots &\vdots &\vdots\\ d_{1m} &d_{2m} &\dots &d_{(n-1)m} &d_{nm} \end{bmatrix} \]
行列の一部を取り出す
行列の一部分を別の行列へコピーするには、以下のようにします。
data = load('data.csv'); n=length(data(1,:)); X = data(:, 1:n-1); y = data(:, n); % m = length(y); %
ここでは、CSVから読み込んだデータセットの左側の(n-1)列をXに代入。一番右の1列をyに代入しています。 この時点で各変数の中身は以下のようになっています。
\[ data= \begin{bmatrix} x_11 &x_{21} &\dots &x_{n1} &y_1\\ x_12 &x_{22} &\dots &x_{n2} &y_2\\ x_13 &x_{23} &\dots &x_{n3} &y_3\\ \vdots &\vdots &\vdots &\vdots &\vdots\\ x_{1m} &x_{2m} &\dots &x_{nm} &y_m \end{bmatrix} , X= \begin{bmatrix} x_{11} &x_{21} &\dots &x_{n1}\\ x_{12} &x_{22} &\dots &x_{n2}\\ x_{13} &x_{23} &\dots &x_{n3}\\ \vdots &\vdots &\vdots &\vdots\\ x_{1m} &x_{2m} &\dots &x_{nm} \end{bmatrix} , y= \begin{bmatrix} y_1\\ y_2\\ y_3\\ \vdots\\ y_m \end{bmatrix} \]
行列の転置
Octave/MATLABで転置するには、シングルコーテーションを使います。
octave:5> theta theta theta = 34.624 30.287 octave:6> theta' theta' ans = 34.624 30.287 octave:7>
列の挿入
行列\(data\)の全行の最初の列に1を挿入するには以下のようにします。
octave:5> data=load("data.csv") data=load("data.csv") data = 6.11010 17.59200 5.52770 9.13020 8.51860 13.66200 7.00320 11.85400 5.85980 6.82330 8.38290 11.88600 ・ ・ ・ ・ ・ ・ 8.29340 0.14454 13.39400 9.05510 5.43690 0.61705 octave:6> m = length(data(:,1)) m = length(data(:,1)) m = 97 octave:7> data=[ones(m,1),data] data=[ones(m,1),data] data = 1.00000 6.11010 17.59200 1.00000 5.52770 9.13020 1.00000 8.51860 13.66200 1.00000 7.00320 11.85400 1.00000 5.85980 6.82330 1.00000 8.38290 11.88600 ・ ・ ・ ・ ・ ・ ・ ・ ・ 1.00000 8.29340 0.14454 1.00000 13.39400 9.05510 1.00000 5.43690 0.61705 octave:8>
データの可視化
Octave/MATLABで、散布図(a scatter plot)を描くためには、以下のようにします。
plot(X(:,1), y, 'x'); % 散布図を描きます ylabel('Amount'); % Y軸のラベルを設定 xlabel('Max temperture'); % X軸のラベルを設定
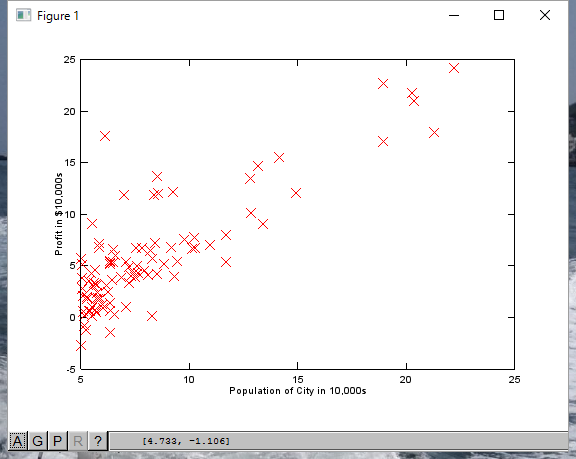
以下は、Courseraの講座で実際に表示したデータです。












![【Amazon.co.jp限定】マトリックス スペシャル・バリューパック (4枚組) [Blu-ray]](http://ecx.images-amazon.com/images/I/51GniNxAVkL._SL160_.jpg)

