C#のラムダ式はAction・Funcと一緒に理解する

photo credit: Imperial Shuttle via photopin (license)
何事も表面的な丸暗記でなく、基礎からキッチリ理解するほうが結果的には早道ですね。
C#のラムダ式に関しては、ActionクラスととFuncクラスをしっかり理解しておけば、それほど難しくはないはずです。
C#のActionクラスは、戻り値のないメソッドを表すクラスで、Funcは戻り値のあるメソッドです。
どちらもジェネリッククラスで、Actionは引数リスト、Funcは戻り値の型と引数リストをジェネリックパラメータで指定します。
Actionはメソッドの動作内容に注目した名前であり、Funcは数学的な関数として評価値を持つ(=戻り値がある)ということですね。
この2つのクラスについては以下のページで詳しく書いていますので参照してください。
C#のラムダ式
ラムダ式の記法的には、以下のような感じ。引数がひとつなら丸かっこは不要とか、波かっこの中身が単一の文なら(複文でないなら)波かっこは要らないとか、いろいろあるんだけど、基本はこちらでOKです。
(name,age) => {
Console.WriteLine(
string.Format(
"{0} is {1} years old",
name, age));
};
型とか指定されていないし、戻り値ってありなの?無しなの?どうでもいいの?てな具合に、全く情緒が安定しない代物ですが・・・
ラムダ式は即時呼び出しできません
JavaScript的にラムダ式を直接呼び出そうとしてエラーになって「何がダメなの?」と混乱しました。 「C#のラムダ式ってJavaScriptの無名関数と一緒でしょ?関数オブジェクトそのものでしょ?」的な思い込みがあったんですね。
でもそれは間違い。C#のラムダ式は、それそのものを呼び出すことができません。
ラムダ式というランタイムオブジェクトは無い
C#のラムダ式は、ActionクラスかFuncクラスのインスタンスを生成するためのものなんですよね。
そもそもこれまで、ラムダ式を見たとき「型が明示されていないのに、どうコンパイルされて実行されているのだ?」と思っていたのですが、正しく動いているコードなら、一見欠落しているように見える引数や戻り値の型情報は、一緒に使われている Action や Func、またはデリゲートで推測可能になってるはず。
ラムダ式はそれらのオブジェクトを生成するために使われるのですが、ランタイムに「ラムダ式」というオブジェクトとして存在しているわけではないということです。
単なる記法、シンタックス・シュガーです
つまり「ラムダ式は、デリゲートやActionやFuncを記述するためのシンタックス・シュガー」であって、それ自体はオブジェクトでもなんでもなく「単なる記法」というわけです。
その証拠に、JavaScriptの即時関数(以下)のようなコードは、C#のラムダ式では実装不可です。コンパイルが通りません。
//JavaScriptの即時関数呼び出し var a = 1; (function(b) { a += b; }(2)); console.log("a:", a);// "a: 3"
C#では、一旦Actionのインスタンスを作ってからでないと実行できません。
なぜかというと、ラムダ式だけでは、引数の型が特定できないからなんですね。
以下のコードでは、Actionクラスによって、第一引数がintであることが明示されている(あえて似せて書いていますので無駄に丸かっこが付いています)ので実行可能となるわけです。
int a = 1; (new Action<int>(b => { a += b; })(2)); Console.WriteLine(string.Format("a: {0}", a));
JavaScriptでの無名関数は関数オブジェクトですが、C#のラムダ式に直接対応するオブジェクトはないってことです。 ちなみにJavaのラムダ式は無名クラスのインスタンスなんですね。 言語によって扱いが異なるのは興味深いがヤヤコシイ。
セルの範囲に入力された最も右の値を得るには「MATCH」を使う

photo credit: Bailey holding a mug via photopin (license)
Crystal
新品 ¥5,499 0個の評価
Amazon.co.jpで詳細を見る
セルの範囲内で、最も右の入力された(空白でない)値を得る には、ワークシート関数 MATCH が使えるんですね(INDEXとMAXも使います)。
かれこれ20年以上エクセルを使い続けていますが、今になって新たなワークシート関数を知って感心するとは思ってもいませんでした。
長年VBAのマクロでやっていましたが計算式だとお手軽です。
そして、このワークシート関数が使えるのはエクセルだけではありません。Google Drive のスプレッドシートでも使えます。
以降で実際の Google スプレッドシートを共有していますので、ご利用ください。
関連記事はこちら↓になります:
takamints.hatenablog.jp
事の発端は進捗管理
先日、個人作業の進捗管理のシートを軽い気持ちで作っていたんですね。
縦方向に作業項目を並べて、横方向には当日から締め切りまでの日付が並ぶ。各項目の進捗状況を日毎に記録するものです。
期限内に全作業がきちんと終了するよう自己管理。日々の状況を把握して、対策打ったり、あきらめたり(笑)、ふさぎ込んだり(!?)ってな使い方です。
客観的マネージメントには数値管理が必要ですし、なにより残工数とか表示しちゃって、予測曲線プロットしたりと、もうデータフェチにはたまらない喜びなわけですよ。理解できないかもしれないけど。
一番右が欲しいのです
作業項目は、1人日(いちにんにち = 一人の人が一日でできる作業)程度に分割しておき、各項目行の日毎のセルに0.5=「今やってます」とか、1.0=「完了した」とか書いていく。
でも、完了したり、そのあと進捗に変化がない日には、同じ数値を入れたくない。手間だし、表としても見にくいし。
なので、各項目の最新の進捗率は、各行の中で、数値が入力されているセルのうち、一番右にあるセルの値を取り出したい。
過去にはVBAのマクロでやってたんですよ。 でも入力時のトリガーで再計算とか結構遅くなりますし、別のシートへ展開しにくいんですよね。 データ管理用のシートに分けたりしてみましたが、行や列の挿入で簡単に破たんしてしまいます。 この辺はホント「エクセルあるある」だと思います。
なので、できれば計算式でやりたいが、そのやり方が分からなかったのです。
過去の自分にググレカス
で、この度ググってみたら以下のサイトが見つかった。
EXCELで、範囲指定した一番右の数値(セル)を返す関数ってありますか?...-Yahoo!知恵袋
detail.chiebukuro.yahoo.co.jp
というか他にもゴロゴロ出てきますやん。しかもそれぞれ、結構古くて2009年とか、7年前の情報です。
なんで今まで検索しなかった?と不思議でしたが、よくよく思い出してみると、ちょうどワタシが管理業務から逃れた離れることになった時期。
当時、このような管理面のことを、(一時的に)ちっとも考えなくなっていたんだな。ダメですね。
MATCHで~す
売り上げランキング: 1,343
売り上げランキング: 26,668
まあ、とにかく、そこで紹介されているのは、以下のような計算式でした。
セル範囲A1:E1に入力されてる最も右の値を得る:
= INDEX ( A1:E1, MATCH( MAX(A1:E1) + 1, A1:E1, 1 ))
INDEX関数
INDEX関数は、セル範囲からインデックスを指定して値を得る関数です。
第一引数がセルの範囲で、第二引数がインデックス。上の式ではA1:E1がセル範囲。MATCH( ... )がインデックスですね。
MATCH関数
で、INDEXの第二引数に指定されてるMATCH関数は、一次元のセル範囲(つまり1行か1列)から検索値にマッチする値が入力されたセルの位置(インデックス)を返す関数です。第一引数が検索値、第二引数がセルの範囲、第三引数が検索の型。
MAX関数
その名の通り、範囲内から最大値を得る関数ですね。
ちょっと待って、なんで最大値を探すのだ?
しかしちょっと待ってくださいよ、上の例では、検索値が、MAX(A1:E1)+1となっていて、セル範囲内の最大値+1となっているではないですか。これ検索してもダメなんじゃ?!と思ったのですが、どうやらミソは第三引数の検索の型。検索の型が1だと、検索値以下の最大値にヒットするのだとか。(だから本来+1する必要はないのだと思います)。しかも省略時のデフォルトが1なので省略してもよいみたい。
まだワカラン。一番右が最大だとは限らんのでは?
しかしまだ、納得できない。釈然としない。最大値の位置を知っても、それが一番右にあるとは限らないのだから、これでは目的の値は得られないのでは?と疑いましたが、なんとMATCH関数の説明に、セル範囲内のデータは昇順にソートされている前提と書かれているんですね。
エクセルのヘルプでは、たまにこういった軽く意味不明の記述がありまして、見るたびに「なんちゅう都合のいい仕様?!www」と嘲笑とか憤慨を覚えていました。
しかし、どうやら、この前提のおかげで、最後まで検索してくれるよう。こういう目的で使いたいから、こんな妙な前提を入れているのかなとか思ったりもしたがはて?。
サンプル(Googleスプレッドシート)
最近気づいたVisualStudio 2015 C# で便利に使える5つの機能
全国的に梅雨も明け、本格的な夏ですね。 自分的には(仕事で)年に一度の恒例のVisualStudioシーズン・イン。 昨年までは冬場が多く、期間は長くても2か月程度。 しかし今年は 6月初めから徐々に動き出して、7月以降に本格化。 期間はトータル4、5か月になりそうです。 終わるころには秋ですね。
例年そんなインターバルでやっているので、VisualStudioやC#の、最新開発状況(環境やプログラミングスタイルなど)になかなか追従できていないのですが、今回は多少期間が長いため、視野がちょっとだけ広くなったか「あ、こんなことができるんだあ」とか「こんな風に書けるのねー」みたいなことが何度かありましたので書いておきます。
あくまでも、自分が知らなくて最近気が付いたってことですので、皆さんご存知なことばかりかも。 しかし、いくつになってもお勉強。新知識には興奮します。

- プロパティ名を指定せずOnPropertyChangedを呼ぶ
- nullチェックの簡略記法
- 自動実装プロパティの初期値設定
- 読み出し専用プロパティを自動実装
- プロパティやメソッドのスニペットを挿入する
売り上げランキング: 42
1. プロパティ名を指定せずOnPropertyChangedを呼ぶ
INotifyPropertyChangedを実装したクラスのプロパティに値を設定されたとき、PropertyChangedイベントを発生させますが、これまで以下のようにプロパティ名を文字列で指定して、OnPropertyChangedメソッドを呼び出していました。律儀にね。
using System.ComponentModel; namespace Application { class ViewModel: INotifyPropertyChanged { public event PropertyChangedEventHandler PropertyChanged; public virtual void OnPropertyChanged(string name) { if(PropertyChanged != null) { PropertyChanged.Invoke(this, new PropertyChangedEventArgs(name)); } } private int _propFoo; public int PropFoo { get { return _propFoo; } set { _propFoo = value; OnPropertyChanged("PropFoo"); } } } }
ところが、プロパティが増えると、そのうち必ず間違えるでしょう?それに、名前を変えたら文字列も変えなきゃならないわけで。 多分おそらく、やってられないですよコレは。
そこで、
[CallerMemberName]を使いましょう
以下のように、OnPropertyChangedメソッドの、プロパティ名称を受け取る文字列引数を、省略可能(既定値は空文字列)にして、[System.Runtime.CompilerServices.CallerMemberName]属性を設定しておくと、引数を省略して呼び出しても、呼び出し元のプロパティ名(以下の例では"PropFoo")が自動的に渡されるのです。
using System.ComponentModel; namespace Application { class ViewModel: INotifyPropertyChanged { public event PropertyChangedEventHandler PropertyChanged; // CallerMemberNameアトリビュートを名前を受け取る文字列引数に指定する。 public virtual void OnPropertyChanged( [System.Runtime.CompilerServices.CallerMemberName] string name = "") { if(PropertyChanged != null) { PropertyChanged.Invoke(this, new PropertyChangedEventArgs(name)); } } private int _propFoo; public int PropFoo { get { return _propFoo; } set { _propFoo = value; //引数を省略して呼び出すと、このプロパティ名"PropFoo"が渡される OnPropertyChanged(); } } } }
これなら、リファクタリングし放題ですねっ。
※ 上の例では、あえて冗長に属性名をフルパスで書いていますが、実際の局面では、いきなり[CallerMemberName]と書いてから(この時点ではコンパイルエラーかも)、[Ctrl]+[.]で、using System.Runtime.CompilerServicesを追加すれば良いですよ。
つまり呼び出し元のメンバ名が渡される
ここの例では、プロパティから呼び出しているのでプロパティ名になっていますが、メソッドから呼び出せば、そのメソッド名が渡されます。 CallerMemberNameの名のとおり、呼び出した側のメンバ名が渡される。
本来イベントとは何の関係もない機能ですが、気付くきっかけが「OnPropertyChangedじゃまくせー」と思って調べていた時だったのでこうなった。 デバッグログを出力するような場合にも有用でしょうね。
2. nullチェックの簡略記法
if文でオブジェクトがnullでないことを確認してから、そのメソッドを呼び出す処理は、さらにシンプルに書けます。 一つ上の例では、イベントのリスナーがいるかどうかを確認しています(以下に抜き出してます)
public event PropertyChangedEventHandler PropertyChanged; public virtual void OnPropertyChanged(string name) { if(PropertyChanged != null) {//←ここ PropertyChanged.Invoke(this, new PropertyChangedEventArgs(name)); } }
長年「こういうものだ」と思っていたので特に不便さは感じていませんでしたが、最近のC#では、以下のように?を使って短く書ける。知ってしまうともう戻れない。
public event PropertyChangedEventHandler PropertyChanged; public virtual void OnPropertyChanged(string name) { PropertyChanged?.Invoke(this, new PropertyChangedEventArgs(name)); }
対象のオブジェクト(上の例ではPropertyChanged)がnullでないならそのままメソッドを呼び出しますが、nullなら何も行わない。
最初、「え?」と思いました。そういえばnull許容型で似た記述をしますが、三項演算子の発展形(省略形?)のようにも思えます。
これは、メソッド呼び出しのための構文ではなく対象オブジェクトがnullかどうかによって、その後のメンバーの参照をするかどうかということです。 そして、以下のようにチェーンできますから、オブジェクトの階層が深い場合は、かなり有利。途中のプロパティやメソッドの戻り値がnullなら、nullとして評価され、それ以降は評価されないということですね(多分)。
Foo?.Bar?.Baz()?.Hoge("Fuga");
メッチャ強力。過去のコードを修正したくなりますね(しないけど)。いやしかし、こりゃ楽でいい。
3. 自動実装プロパティの初期値設定
地味ではあるけど、これも由。
自動実装プロパティに特定の初期値を与えるためには、以下のように、コンストラクタで値を設定しなくてはならなかったと思っていましたが、
//従来の自動実装プロパティを持つクラス class Foo { public int Bar { get; set; } public Foo() { Bar = 999; } }
プロパティ宣言部分で値を設定できる(以下)ようになっていました。
//最新式(笑)の自動実装プロパティを持つクラス class Foo { public int Bar { get; set; } = 999; }
これも楽です便利です。
自動実装で楽しているにもかかわらず、コンストラクタを別途定義するとかアホちゃうかと潜在的に思っていましたが、やっと報われた(謎)。
4. 読み出し専用プロパティを自動実装
売り上げランキング: 79,718
もうひとつ自動実装プロパティネタ。
GetterがパブリックでSetterはプライベートというプロパティは自動実装できないものだと思い込んでいて、常々以下のように書いていました。
class Foo { private int _bar = 999; public int Bar { get { return _bar;} } }
でも、以下のように書けるのだとか。
class Foo { public int Bar { get; private set; } = 999; }
これは、自分が知らなかっただけかな。
5. 自動実装プロパティのスニペットを挿入する
プロパティを新設するとき、全部自分でキー入力していましたが、エディタでpropと入力して、[Tab]を2回叩けば、とりあえずint型のMyPropertyという自動実装プロパティが挿入されますね。
ほかにも便利なスニペットがあるかもしれん。いろいろ探し歩いてみます。
売り上げランキング: 4,385
Visual Studio 2015 Update 3 適用でテストウィンドウに例外発生 ⇒ 言語設定を英語にすれば治りますけど・・・
何も考えずに更新プログラムとか適用しちゃうの良くないねってな典型的なことをやらかしちゃって、お恥ずかしい限りですけど、書いておきます。
いくつになってもお勉強です。

2016-08-03 追記:Update 3へのパッチが本日適用可能になっており、日本語環境でのテストウィンドウの例外は解消しました。結果的には問題なかったのですが、インストール直後のVisual Studioの起動が大変遅く、日本語に切り替えてからは、三回ぐらい、ソリューションの読み込みが「応答なし」で失敗しました。しかし、この現象はパッチの影響ではないかもしれません。Windows 10の「Antimalware Service Executable」の問題と関連していたかも。
要約すると
- VisualStudio Community 2015の日本語環境に Update 3 を適用。
- ソリューションを開くとテストウィンドウの初期化時エラー。ユニットテストが表示されない。
- 日本語環境では回避不能。言語設定を英語にすればエラーは発生しないようです。
ということで、本質的な解決にはなっていませんが、エラーの内容や、対処手順を以下に書いておきました。
発生した現象
VisualStudio Community 2015で、ソリューションを開くと「Update 3が利用可能」と通知され、普段からあまり何も考えていないので、つい更新しちゃったのですが、その後、ソリューションを開いたら以下のメッセージが表示されてダメだこりゃ。
パーツ "Microsoft.VisualStudio.TestWindow.UI.TestWindowToolWindowControl" の初期化中に例外がスローされました。
画面はこちら
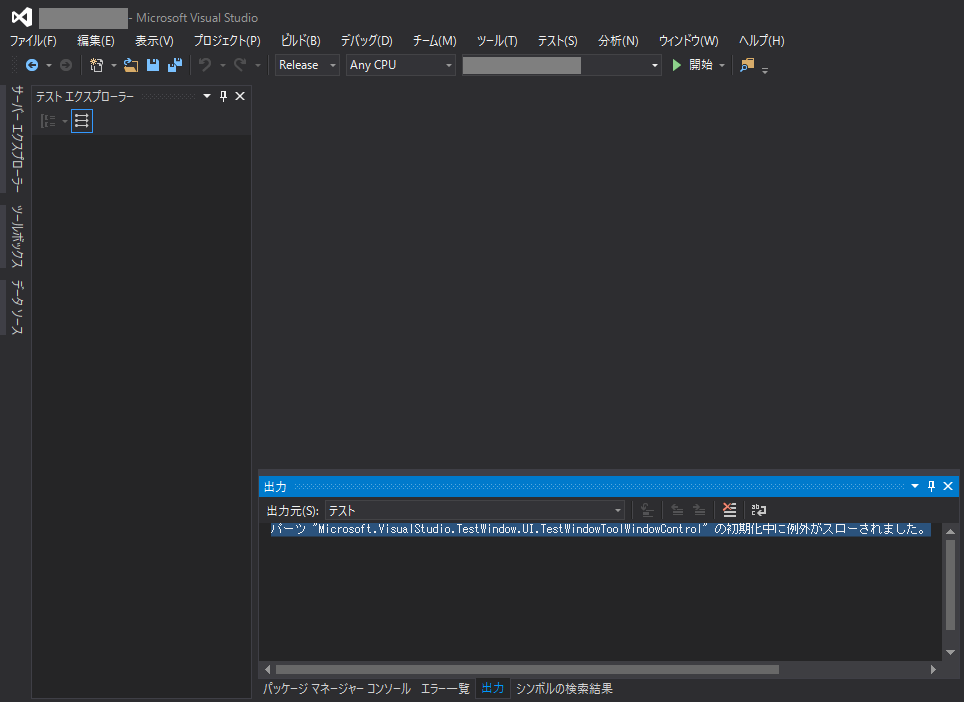
なんと、ユニットテストのウィンドウの中身(テストの一覧が表示されるところ)が空っぽですよ。ダメじゃないかVisualStudio。
「全てのテストを実行」しても、結果がわからないどころか、本当に実行されているかどうかも分からない。
言語設定を英語にすれば回避可能、だが・・・
エラーメッセージ(↑)丸ごと検索で、たった一件、Visual Studioのページがヒット。どうやら日本語環境では不可避なようです。で、英語版なら大丈夫だと。
仕方がない。とりあえず「英語版に切り替えよう」と、メニューバーから[ツール]-[オプション]でオプションダイアログ表示して、左側のツリーから[環境] > [国際対応]とポイント、右の[言語]ドロップダウンから[英語]・・・
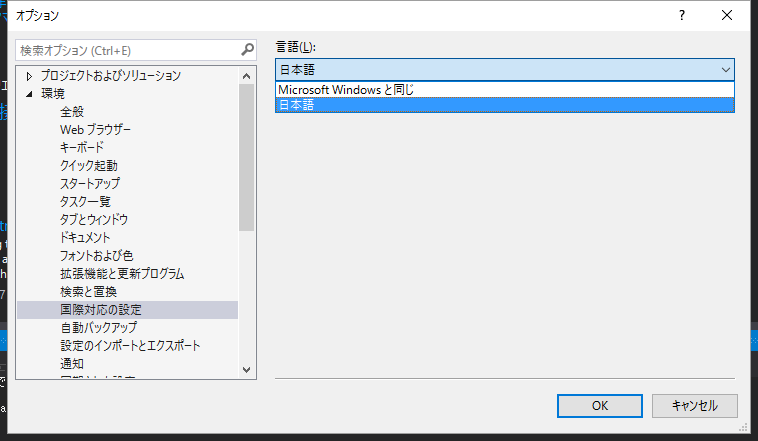
選べないです。そういうもんなんですね。日本語パックを外せば英語になるのかと思ってましたが違ってました。
そこで英語の言語パックをダウンロードしてインストール
面倒だけど同ダイアログの「追加の言語を取得する」というリンクをクリックして、
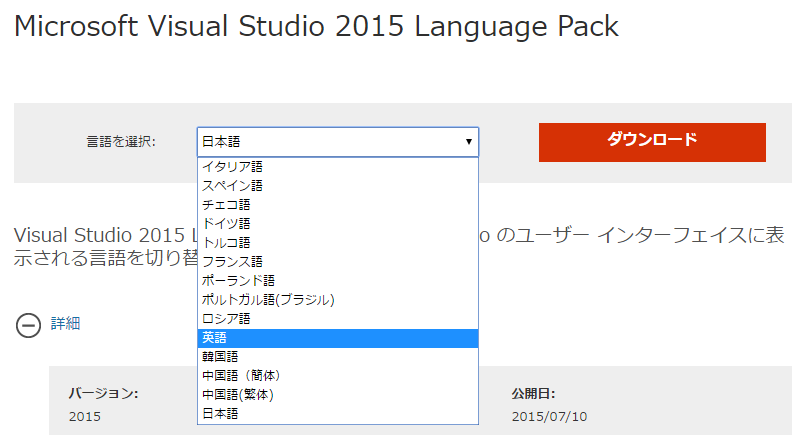
ドロップダウンから「英語」を選び(ページが更新されます)
Downloadをクリックして、
ダウンロードされたvs_langpack.exeを実行してから画面に従いインストール。
LanguageをEnglishにChangeすると
やっとこ、オプションダイアログで言語のコンボから、「English」が選べるようになりましたよっと。
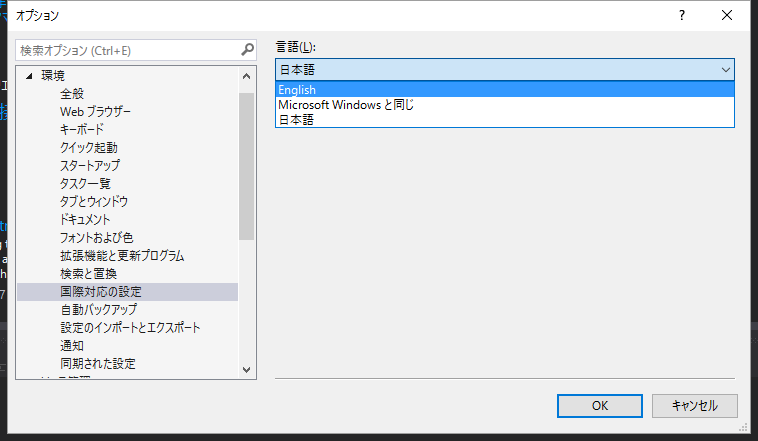
そして、VisualStudio 再起動。
あらおめでたい
英語だ英語だ・・・
確かにエラーは出ませんでした。
しかしだよ
全部英語で表示されると若干(かなり)使いにくい。 感覚的に操作できないというか、ずらりと表示されるコンテキストメニューとか、目を皿のようにして一生懸命読まないといけない感じ。 人間の視覚と言語って密接にかかわっているのだなあと感心しますが、なによりこのバグ治ってほしいわ。
その他
あと、言語設定に関係ないですけど、自分の中でも未確認情報ですが Update 3を入れた後、ビルド実行やデバッグ実行に失敗したりしなかったりと、統合環境の動作が不安定な気がします。
よくわからないですけどね。
Update 3 では、Update 2でのメモリの大量使用が改善されているようで、なんとなく起動が早い気がします(スプラッシュ画面だけ延々表示されてる時間が短い)。ユニットテストをしない人や、英語に違和感がない人は、気にせず更新すれば幸せかもしれません。
参考サイト
- [修正済み] Visual Studio 2015 "日本語" の環境に最新の更新 (KB3165756) を適用するとテストエクスプローラーが機能しなくなります
- Download Microsoft Visual Studio 2015 Language Pack from Official Microsoft Download Center
- .NET TIPS:Visual Studio:メニューなどの表示言語を切り替えるには? - @IT
こちらもどうぞ ― Visual Studio / C# / WPF 関連記事
【機械学習基礎固め】線形回帰(Linear Regression)の初歩的ポイントを再確認して書いておく
昨年の今頃、CourseraのMachine Learningの講座を受講しましたが、 急いで詰め込んだ情報ってのは、やっぱり消えていくのも早いようです。

当時、仕事で炎上案件の火消し作業に関わっておりまして、 深夜に帰宅し、晩御飯をいただきながらネットで受講。 字幕付きの英語のビデオを視聴して、週一で課題提出というサイクル。 特に後半は睡眠時間の確保が難しくなり気持ち的にも駆け足で、次第に「講座を終わらせること」が目的になっていました。
どうにか8月末に修了したけど、達成感とか感じる前に「炎上案件なんだかなあ?」な状況で、学習内容はすぐに蒸発。 理解が曖昧なところが起点になって、急速に知識の最小単位の輪郭がぼやけていくんですよ怖い怖い。
てなことで、一年経って新たな気持ちで講座のテキストや受講中に取ったノートをめくりながら復習中。 気長にじっくりポイント押さえて経年劣化の激しいニューラルネットワークにしっかり刻みつけていきたいなあと思っております。 ただし、ここに書いているのは私個人が理解したと思っているものに過ぎませんので気を付けてくださいね。
以下の記事では、実際に線形回帰をやってみています。結果はいまいち満足していないですが、ご参考に。
ちなみに、数式はMathJax使って書いています。LaTeXの書式で数式を書けば、きれいに整形してくれるスクリプト。まともに使ったことがなかったのですが、なかなか便利。ブログはMarkdownで書いているので _や^を\でエスケープしないといけないようで少々わずらわしいのですが、理屈が分かればなんとかなります。
やはり、いくつになってもお勉強です。
- Courseraの権利を侵害するのはまずいので、本記事の内容は箇条書きに毛が生えた程度のものです。またテキストの内容をそのまま書いたりもしませんよ。
- 詳しい内容を知りたい方は、ぜひとも同講座を受講してみてくださいね。非常に興味深い内容です。
- 受講のためには、少なくとも、行列演算の基礎を理解している必要があると思います。それと課題や試験の文章が英語なので、辞書片手にでもよいので英文の読解力がある程度必要です。講義の動画では日本語の字幕が付きますが、私が受講したときは、字幕が追い付いていない場面が何か所かありました。また、字幕を読んでいる時は、表示されてる式を見逃すということも。ヒヤリングができるに越したことはないですよ。
- まあしかし、無料なので気軽に受けてみるのもアリかもしれない。構えて撃ってから狙いましょう。
ところで、Octave for Windowsの不便な点
ハナから横道に逸れますゴメンナサイ。先日からWindows 10でMinGW/MSYSからOctaveを使っていますが、不便な点が以下3つ。
gccでビルドすれば解決できそうな気がするのですが、またそのうち。
線形回帰(Linear regression)とはなんであるか
線形回帰(分析)とは、線形モデルによる回帰分析ということらしい。データセット内のデータの相関をモデル化する方法・・・かな?
線形モデルは、以下のような式で定義されます(Wikipediaから引用)。
\[ Y=\beta_{0} + \beta_{1}X_{1} + \beta_{2}X_{2} + \dots + \beta_{p}X_{p} + \varepsilon \]
\[ \begin{eqnarray*} Y & : & 出力値\\ X_i & : & 入力値\\ \beta_i & : & 線形モデルのパラメータ \end{eqnarray*} \]
実は自分、\(\varepsilon\)が何物なのか理解できていません。切片は\(\beta_{0}\)だし・・・。 まあ、とにかく、与えられたデータセットに対して、このような線形モデルの仮説を立てて、そのパラメータである\(\beta_i\)を決定しましょうということですね。
例えば、日毎の最高気温と湿度、アイスキャンデーの売上額というデータセットがあって、 ある日の天気予報から売上予測を行う場合、 最高気温は\(X_1\)、湿度は最高気温は\(X_2\)、売上額は\(Y\)ですが、\(\beta\)の値がわからない。 データセットは観測(測定)データであり、計算して出したものではありませんから。
てことで、与えられた実際のデータセットを線形回帰分析して、\(\beta_{0 \dots 2}\)をちょうどよい値に調整するということですね。
参考サイト
仮説関数(hypothesis function)
仮説関数。これは、与えられた問題を解決するための関数であって、いわゆる上で書いている線形モデルそのものですね。 既知のデータから作成された入力と出力の相関を表すための式ですから、実データXを与えれば実データY(に近い値)を出力し、未知の入力に対しても仮説に基づいた値を出力する。つまり、これを使って予測ができるということになる。
線形回帰では仮説関数が線形モデルになっているということですね。
上のWikipediaからの引用では、モデルのパラメータを\(\beta\)としていましたが、Courseraの講座では一貫して\(\theta\)で統一されていました。 自分にとってはすでにこちらのほうがなじみがあるので、以降\(\theta\)で通します。
講座では、以下のような単純な仮説が立てられていました。(\(x\)が入力。\(y\)は仮説に基づいて出力される値)
\[ y=\theta_0 + \theta_1x_1 + \theta_2x_2 \]
この仮説関数は、\(x_0 = 1\)と置くと以下のように書けます。
\[ y=\theta_0x_0 + \theta_1x_1 + \theta_2x_2 \]
そしてこれは行列を使用して以下のように記述できます。日常的に行列を扱っていないので、上の式を見てすぐ行列演算に結び付けられないが、それも慣れなのだろう。
\[ h_\theta(x) = \theta^{T}x = \theta_0 + {\theta_1}x_1 + {\theta_2}x_2 \]
\(\theta^{T}\)のTは転置(Transpose)の意味です。以下参照。
\[ \theta^T = {\begin{bmatrix} \theta_0\\ \theta_1\\ \theta_2 \end{bmatrix}}^T = \begin{bmatrix} \theta_0 &\theta_1 &\theta_2 \end{bmatrix} \]
\(\theta_{0 \dots 2}\)が、線形モデルのパラメータ(初期値は1とか乱数とか)。後述の勾配降下法によって、コスト関数の出力が少なくなる(つまり誤差が少ない)値を決定するのです。これが線形回帰分析ですね。
※ \(x_1\)の添え字の1は、最初の入力値という意味であり、データセットのインデックスではありません。
コスト関数(Cost function)
コスト関数は、仮説関数がどれくらい的を得ているかを表します。 実データと理論値の差分の絶対値に関する値で。 線形回帰では、たいてい以下の式で定義されるらしく、全サンプルの二乗平均誤差に比例する値です。
\[ J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} ({{h_\theta}{(x^{(i)})-y^{(i)}})^{2}} \]
下図は、Courseraの講座で描いたコスト関数の三次元グラフです。縦方向がコストです。

勾配降下法(Gradient Descent)
売り上げランキング: 34,160
線形回帰の目的は、コスト関数の結果を最小化する\(\theta\)を見つけること。 そのために、勾配降下法を使用して、線形回帰のパラメータである\(\theta\)を、データセットにフィットさせます。 勾配降下法にも種類があるようですが、最初はバッチ勾配降下法(Batch Gradient Descent)が取り上げられていました。 これまた「それが何たるや?」は、よくわかっていないので、そのうち確認してみます。 とりあえず、コスト関数\(J(\theta)\)の出力を最小化する\(\theta\)を見つける方法の一つということで。
その名のとおり、坂を下りていくようなアルゴリズム。x軸を\(\theta_0\)、y軸を\(\theta_1\)、z軸をコスト関数の出力として、x-yをスイープして描いた三次元のグラフについて、特定のx-y位置からz成分が小さくなる方向へ徐々に移動(\(\theta_0\)と\(\theta_1\)を更新)していくものです。最終的に逆向きのピークに落ち着くというわけですね。
下図は、講座の中で、コスト関数の等高線を描いたものです。赤い×印が一番コストの低い場所です。
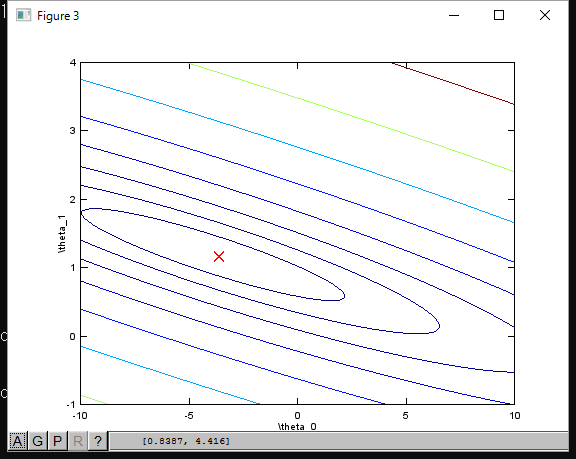
このように、データを可視化して、処理が正しく行われているかを確認する必要があります。 θの要素数が多い場合は全てを使ってグラフを描けませんが、特定の軸を抜き出して描けばよいです。勾配降下に関する考え方は同じです。 また、複雑な仮説関数では、くぼんでいるが、一番低いわけではない場所に落ち込んでしまう場合がありますが、そういった問題の回避方法や、速めに収束させるためのテクニックなどが講座で細かく紹介されていました。
線形回帰のパラメータθを繰り返し更新する
実際の演算ではθをスイープするのではなく(演算量が大きすぎるし意味がない)、ある出発地点を選んで、その場所のコスト/θの傾きに応じて、コストが低い場所へ移動することを繰り返します。
ある地点の傾きが関わってくるので、偏微分といった(自分的に)難しい内容も関連し、きちんと理解していませんが、とりあえず、個々の繰り返しでθを更新するのは、以下の式を使うらしい。
\[ \theta_j := \theta_j-\alpha \frac{1}{m} \sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x^{(i)}_j \]
- \(i\)は、データセットのインデックス。
- \(j\)は、線形回帰パラメータの添え字。
- \(\alpha\)は学習率(learning rate)を表す値です。小さな値では\(\theta\)の収束が遅くなり、大きな値だと早く収束します。
ここで大切なのは、\(\theta\)の全要素を同時更新するということです。\(\theta\)の要素がひとつでも変化すると、仮説関数 \(h_\theta(x^{(i)})\) は別の式になり、その値は変化してしまいますが、全要素を更新するまで仮説関数は変化すべきではないということです。
繰り返しによって線形回帰のパラメータ\(\theta_j\)は、コスト関数\(J(\theta)\)を最小化する値に近づいていきます。
Octave/MATLABの使い方
CSVを読み込む
データセットがカンマ区切りのテキストデータとして用意されている場合、Octave/MATLABで以下のようにして行列に読み込みます。
data = load('data.csv'); % カンマ区切りのテキストデータを読み込む
例えばCSVにn列m行のデータがあるなら、dataの中身は以下のようになっています。
\[ data= \begin{bmatrix} d_11 &d_{21} &\dots &d_{(n-1)1} &d_{n1}\\ d_12 &d_{22} &\dots &d_{(n-1)2} &d_{nn2}\\ d_13 &d_{23} &\dots &d_{(n-1)3} &d_{n3}\\ \vdots &\vdots &\vdots &\vdots &\vdots\\ d_{1m} &d_{2m} &\dots &d_{(n-1)m} &d_{nm} \end{bmatrix} \]
行列の一部を取り出す
行列の一部分を別の行列へコピーするには、以下のようにします。
data = load('data.csv'); n=length(data(1,:)); X = data(:, 1:n-1); y = data(:, n); % m = length(y); %
ここでは、CSVから読み込んだデータセットの左側の(n-1)列をXに代入。一番右の1列をyに代入しています。 この時点で各変数の中身は以下のようになっています。
\[ data= \begin{bmatrix} x_11 &x_{21} &\dots &x_{n1} &y_1\\ x_12 &x_{22} &\dots &x_{n2} &y_2\\ x_13 &x_{23} &\dots &x_{n3} &y_3\\ \vdots &\vdots &\vdots &\vdots &\vdots\\ x_{1m} &x_{2m} &\dots &x_{nm} &y_m \end{bmatrix} , X= \begin{bmatrix} x_{11} &x_{21} &\dots &x_{n1}\\ x_{12} &x_{22} &\dots &x_{n2}\\ x_{13} &x_{23} &\dots &x_{n3}\\ \vdots &\vdots &\vdots &\vdots\\ x_{1m} &x_{2m} &\dots &x_{nm} \end{bmatrix} , y= \begin{bmatrix} y_1\\ y_2\\ y_3\\ \vdots\\ y_m \end{bmatrix} \]
行列の転置
Octave/MATLABで転置するには、シングルコーテーションを使います。
octave:5> theta theta theta = 34.624 30.287 octave:6> theta' theta' ans = 34.624 30.287 octave:7>
列の挿入
行列\(data\)の全行の最初の列に1を挿入するには以下のようにします。
octave:5> data=load("data.csv") data=load("data.csv") data = 6.11010 17.59200 5.52770 9.13020 8.51860 13.66200 7.00320 11.85400 5.85980 6.82330 8.38290 11.88600 ・ ・ ・ ・ ・ ・ 8.29340 0.14454 13.39400 9.05510 5.43690 0.61705 octave:6> m = length(data(:,1)) m = length(data(:,1)) m = 97 octave:7> data=[ones(m,1),data] data=[ones(m,1),data] data = 1.00000 6.11010 17.59200 1.00000 5.52770 9.13020 1.00000 8.51860 13.66200 1.00000 7.00320 11.85400 1.00000 5.85980 6.82330 1.00000 8.38290 11.88600 ・ ・ ・ ・ ・ ・ ・ ・ ・ 1.00000 8.29340 0.14454 1.00000 13.39400 9.05510 1.00000 5.43690 0.61705 octave:8>
データの可視化
Octave/MATLABで、散布図(a scatter plot)を描くためには、以下のようにします。
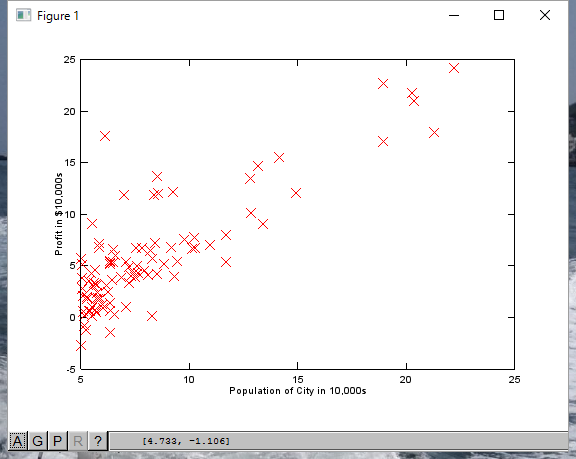
plot(X(:,1), y, 'x'); % 散布図を描きます ylabel('Amount'); % Y軸のラベルを設定 xlabel('Max temperture'); % X軸のラベルを設定
以下は、Courseraの講座で実際に表示したデータです。



![Excel 最強の教科書[完全版]――すぐに使えて、一生役立つ「成果を生み出す」超エクセル仕事術](https://images-fe.ssl-images-amazon.com/images/I/41wHkFBnSwL._SL160_.jpg)


























![【Amazon.co.jp限定】マトリックス スペシャル・バリューパック (4枚組) [Blu-ray]](http://ecx.images-amazon.com/images/I/51GniNxAVkL._SL160_.jpg)

